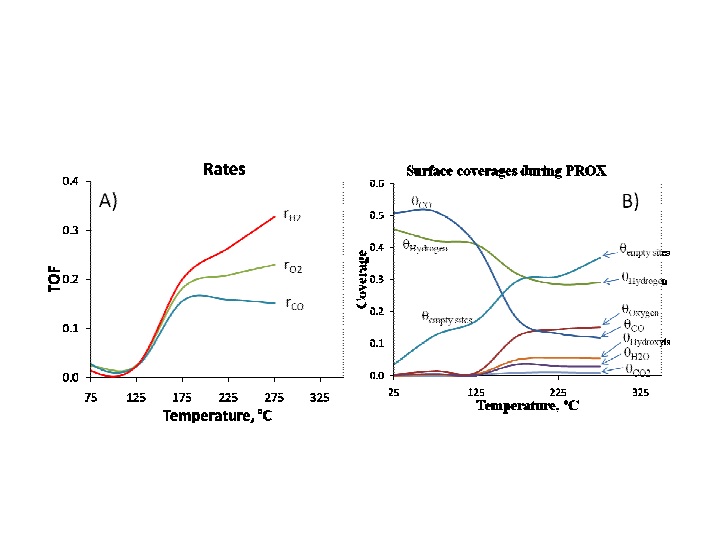
Introduction The extended application of Monte Carlo (MC) simulations to the field of catalysis is advantageous because it can incorporate structural parameters such as crystallites size and sites with different reaction rates. MC simulations are often restricted by the differences observed in the magnitudes of rates of the reactions involved. On catalytic surfaces, multiples events take place at the same time (adsorption, desorption, reactions, etc.) but at significant different rates. The rates of these processes are used to calculate each event probability and, if large differences are observed in the rates, then large differences will also be observed in the probabilities. Thus, events having very low probability will not occur in the MC simulation although they might occur in real catalytic systems. Large differences in reaction rates observed in nature are due to the time scale at which they take place. Such property, when reflected in differential equations with very different eigenvalues, is known in numerical analysis as stiffness. Here we present a general new approach for conducting MC simulations of stiff catalytic reactions systems. This new method, based on the sampling of normally distributed rate probabilities, is applied to the simulation of a system of stiff differential equations and compared with an MC simulation with and without a normal distribution and also to experimental results obtained during the preferential oxidation of CO reaction (PROX). Most of the rate constants were obtained from literature with the exception of the surface reaction of adsorbed CO and hydroxyls. MC Method and Experiments The reaction simulated is the preferential oxidation of CO in the presence of hydrogen (PROX) on a Pt supported catalyst. For the Monte Carlo PROX simulation, each Pt particle was modeled as a truncated hexagonal pyramid [1, 2]. The support was assumed to be a thin square plate with 1 to 69 crystallites randomly distributed onto it, and with each crystallite having between 2 to 7 layers of atoms. The crystallite size studied ranged from 8 to 27 Å. The size of each crystallite was varied by changing the number of total atoms that conforms each crystallite. The reaction system included the adsorption and oxidation of adsorbed CO and hydrogen, and formation and oxidation of adsorbed hydroxyl species. The normalized probabilities of each event were calculated using the logarithmic value of the rates instead of their numerical values. Experimentally, 1%Pt/Al2O3 catalysts were prepared by wet impregnation using tetraammineplatinum (II) nitrate (Aldrich) as precursor. After impregnation the catalysts were calcined at 300, 400, 500, and 600 ºC. These different calcination temperatures led to Pt dispersions of 70, 66, 63, and 30%, respectively. Pt dispersions were measured by CO chemisorption assuming a CO/Pt ratio of 1. The reaction mixture had a composition of 0.8% CO, 0.8% oxygen, and 51% H2, with He as balance, and was added at a total flow rate of 195 cc/min. Reaction rates were measured in a recycle reactor and turnover frequencies (TOF) were calculated based on Pt dispersion. Results and Discussion Results are first presented comparing normalized and non-normalized rates showing that no convergence is attained without normalizing the rates. Figure 1 shows the results of simulating the PROX reaction using a Monte Carlo algorithm based on normally distributed probabilities of the individual rates (adsorptions, desorptions, reactions, etc). Figure 1A shows the rates of consumption of H2, O2, and CO, expressed as turnover frequencies (TOF). The TOF from the simulations are in close agreement to the experimental results (not shown). The coverages shown in Figure 1B indicate that at low temperatures the surface is mainly covered by CO and H2. As the temperature increases CO gradually reacts and desorbs while the coverage of H2 only shows slight variations due to the higher partial pressure of H2 than CO and O2. As CO desorbs more sites become available for O2 adsorption. The increased oxygen coverage favors reactions with hydrogen, reflected in higher coverage of water and hydroxyls. The higher population of hydroxyls above 150ºC leads to an increase in the CO2 production. This is in agreement with the PROX mechanism where surface hydroxyls react with surface CO to produce CO2. However, as the temperature increases more hydrogen is oxidized to water (undesired reaction) and therefore, the selectivity to CO2 gradually decreases. The MC simulation of the PROX reaction indicates that the adsorption of oxygen is the rate limiting step. The oxygen adsorption occurs more efficiently as the dispersion of Pt decreases due to the increase of sites located on the more active (111) faces which due to its packing of 6 near neighbors per Pt atom, which in turn facilitates the dissociative adsorption of oxygen. The size of the (111) faces increases on larger particles and therefore oxygen adsorption occurs more efficiently on larger particles due to the presence of more accessible sites on (111) faces. The MC simulation results agree with experimental observations and explain the role of crystallite size in the observed reaction TOF. Significance The new method presented here represents a simple and straightforward approach to solve stiff reaction systems. Although the simulation of the PROX reaction has been presented as a case study, the method is not restricted to this example and can be extended to other complex reactions occurring of catalytic surfaces. Acknowledgments The support of this work by a Bayer Postdoctoral Fellowship in Environmental Chemistry through the Center for Environmental Science and Technology at the University of Notre Dame is gratefully acknowledged. References 1. F. Gracia , and E.E. Wolf, Chem. Eng. Journal, 2001. 82: p. 291-301. 2. F.J. Gracia , and E.E. Wolf, Chemical Engineering Science, 2004. 59: p. 4723-4729.