An Extended CEOS/ Zero-Pressure Mixing Rule and its Application to Phase Equilibrium Calculation

Gang Xu, David Van Peursem and David Bluck

Invensys/SimSci-Esscor,

26561 Rancho Parkway South, Suite 100, CA, 92630

  Abstract:

An extension of a recent CEOS/zero-pressure mixing rule developed by Twu, Coon, and Bluck (TBC) 1998 has been introduced. This extended new TBC model maintains the original accuracy over a large amount of strongly non-ideal mixtures without requiring additional binary interaction parameters. It also extends the capability of including light compounds (like CO2, CH4 …) into mixtures with strong hydrogen bounding, association effects. Introduction:

CEOS/zero-pressure mixing rule developed by Twu, Coon, and Bluck (TBC) presents extremely high accuracy for highly non-ideal mixtures without requiring additional binary parameters. The original TBC model has been tested against extensive binary mixtures from various literatures like DECHMA with extremely accuracy. However, a key assumption on the existence of liquid volume at zero pressure kept it from being extensively applied across thermodynamic applications, and remains as a model flaw. In this paper, the original TBC and a literature extension on overcoming the model flaw for the existence of the liquid volume at zero pressure will be briefly reviewed, followed by a general extension of TBC defined as post-processing, which completely removes the model flaw without increasing the model complexity.

Review on TBC:

Listed here are the same expressions for the energy and volume parameters and as in Twu et. al, 1998

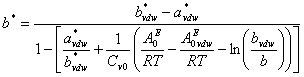                              (1)

                                (2)

 in the equations above represents the excess Helmholtz energy at zero pressure evaluated from a cubic equation of state using the van der Waals one-fluid mixing rule for  and .  represents the excess Helmholtz energy at zero pressure calculated from an activity model.  is calculated from the smallest root of  using the selected cubic equation of state (such as SRK or PR) at zero-pressure. Detail formulation of  can be written as

                                                             (3)

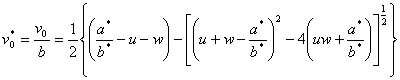      (4)

In order for  to have a real root, equation (4) must satisfy

                                                  (5)

However, two key issues arise here. First, equation (5) is not guaranteed in general; second, even with equation (5) satisfied, numerical instability may still exist in the calculation of . To understand these two issues, calculation of  from a cubic equation of state has to be addressed here. In general, excess energy model is expressed as

           (at zero pressure)                                (6)

where  is the fugacity coefficient of component  in the mixture, and  is the fugacity coefficient of pure component .

It has been verified that the whole TBC mixing rule would most-likely blow-up numerically if inconsistent compressibility roots are selected for  and , which either leads to unphysical phase equilibrium solutions, or causes convergence issue. This happens in the liquid phase when one of  and  has identical “cubic” root of the compressibility, while the other one has distinguishable cubic compressibility roots. It is very interesting that all the tested systems in Twu, et. al. (1998) have distinguished compressibility roots for both  and  at their testing conditions, which allows the root selection to be consistent. Unfortunately, this is not always happening.

Post-processing Algorithm:

We introduce here an complete extrapolating technique which fully extended TBC mixing rule towards high-temperature and high-pressure region. Theory and tested examples will be included to further explain this new model.

  References

 [1]      Chorng H. Twu, John E. Coon, David Bluck, “Comparison of the Peng-Robinson and Soave-Redlich-Kwong Equations of State Using a New Zero-Pressure-Based Mixing Rule for the Prediction of High-Pressure and High-Temperature Phase Equilibrium”, I&ECR, 1998, 37, 1580-1585.